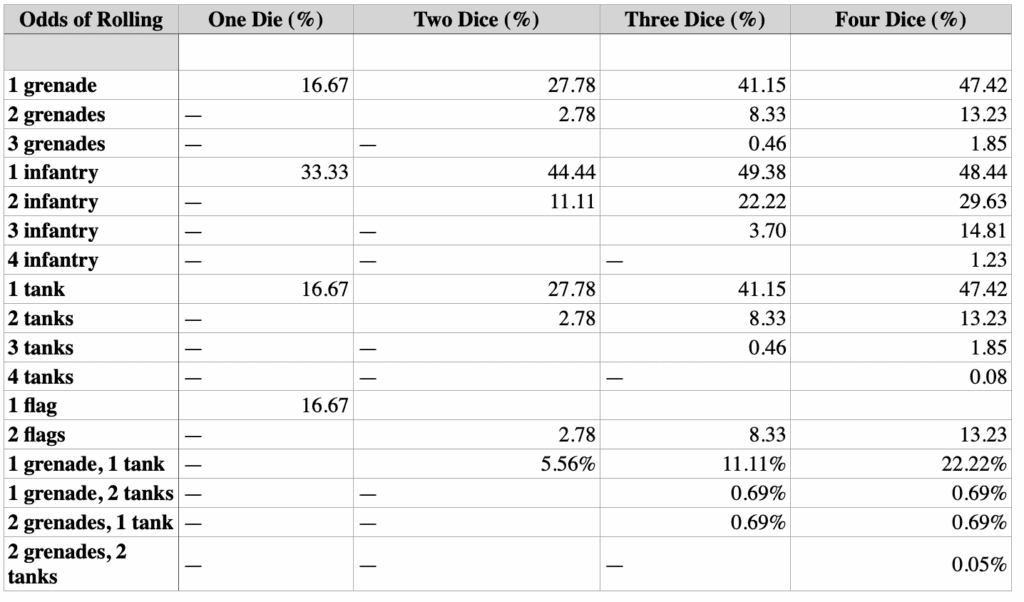
Dice Percentages
When rolling just one Die
Infantry – 33%
Armor – 17%
Grenade – 17%
Star – 17%
Flag – 17%
Against Artillery
| Odds of Destroying both Artillery figures with: | |
| Two Dice | 2.8% |
| Two Dice (w/ Star) | 11% |
| Three Dice | 7.4 % |
| Four dice | 13% |
Against Artillery - No Retreat
| Odds of Destroying a No Retreat Artillery with: | |
| Two Dice | 11% |
| Two Dice (w/ Stars) | 25% |
| Three Dice | 26% |
| Four Dice | 41% |
Average number of single dice rolls to eliminate one no-retreat artillery figure = 3 rolls (1/3 chance for each either Grenade or Flag).
Average number of single dice rolls to eliminate a complete two-figure no-retreat artillery unit = 6 rolls.
Against Armor
| Odds of rolling at least one hit against armor | |
| One Die | 33% |
| Two Dice | 55% |
| Three Dice | 70% |
| Odds of rolling at least two hits against armor | |
| Two Dice | 11% |
| Three Dice | 26% |
| Four Dice | 41% |
| Odds of rolling at least three hits against Armor | |
| Three Dice | 3.7% |
| Four Dice | 11% |
Against Armor - No Retreat
( Note that an attack against a No-Retreat Armor has the same odds as an attack against Infantry with Retreat. )
| Odds of rolling at least one hit against no-retreat armor | |
| One Die | 50% |
| Two Dice | 75% |
| Three Dice | 87% |
| Odds of destroying a 3-figure no-retreat Armor unit | |
| 3 Dice | 12.5% |
| 4 Dice | 31% |
Against Infantry
| Odds of rolling at least one hit against Infantry | |
| One Die | 50% |
| Two Dice | 75% |
| Three Dice | 87% |
| Four Dice | 94% |
| with a Sniper | 66% |
| Odds of rolling at least two hits against Infantry | |
| Two Dice | 25% |
| Three Dice | 50% |
| Four Dice | 69% |
| Odds of rolling at least three hits against Infantry | |
| Three Dice | 12.5% |
| Four Dice | 31% |
| Odds of destroying a complete Infantry unit | |
| Four Dice | 6% |
Against Infantry - No Retreat
| Odds of rolling at least one hit against no-retreat Infantry | |
| One Die | 66% |
| Two Dice | 89% |
| Three Dice | 96% |
| Odds of destroying a complete no-retreat Infantry unit | |
| Four Dice | 20% |
Odds for an Armor Overrun
| Against a single Infantry figure | |
| 1D | 58% |
| 2D | 83% |
| 3D | 93% |
| 4D | 97% |
| Against a single Armor figure | |
| 1D | 44% |
| 2D | 70% |
| 3D | 83% |
| 4D | 90% |
Odds for a Barrage
| Artillery | 1 figure | 52% |
| Infantry | 2 figures | 69% |
| Armor | 2 figures, w/o retreat | 69% |
| Infantry | 3 figures, w/o retreat | 59% |
| Armor | 3 figures, w/o retreat | 31% |
| Artillery | 2 figures, w/o retreat | 41% |
( stats from Memoir 44: Tactic & Strategy Guide, Alexis Beuve and ChatGPT)
Odds of a Flag Roll
| 1 Die | 17% |
| 2 Dice | 31% |
| 3 Dice | 42% |
| 4 Dice | 52% |
Odds Against a Tiger Tank
Some scenarios, like Villers-Bocage, require the Allies to attack the Axis Tiger Tanks. This requires TWO rolls to win; the first roll is the standard Armor or Grenade, but the second one must be a Grenade in order to score a hit and destroy the Tiger.
Since the two rolls are independent, we multiply their probabilities:
P(First roll is Armor or Grenade AND second roll is Grenade)
The probability of rolling, for one die, an Armor or Grenade on the first roll, and a Grenade on the second roll, is 1/18 (≈5.56%).
( Please be advised: Most of these percentages were calculated with ChatGPT. )
